In a recent article published in Physical Review Letters (PRL 118, 117202 (2017)), researchers from the Nanomagnetism group at nanoGUNE reported so-far unknown anomalies near dynamic phase transitions (DPTs). Such anomalies do not exist in corresponding thermodynamic phase transitions (TPTs), and thus, they constitute a distinct difference between DPTs and TPTs, even though their equivalency was the key outcome of more than two decades of research by many groups around the globe.
The study of dynamic behavior and kinetic pattern formation in interacting systems is a crucially important aspect of science, given that they are present in such diverse areas as laser emission, the formation of sand dunes or brain activity. Correspondingly, the study of non-equilibrium dynamic phenomena is of utmost importance, and its detailed understanding crucially relies on appropriate models. One of these models is the widely used kinetic Ising Model (kIM), which can exhibit qualitatively different types of dynamic behavior, including dynamic phase transitions, despite its simplicity. After more than two decades of research using the kIM, consensus emerged that the properties of DPTs are truly analogous to those of TPTs. The new work by the nanoGUNE team, however, revealed that these similarities between dynamic and thermodynamic phase transitions are far more limited than previously thought.
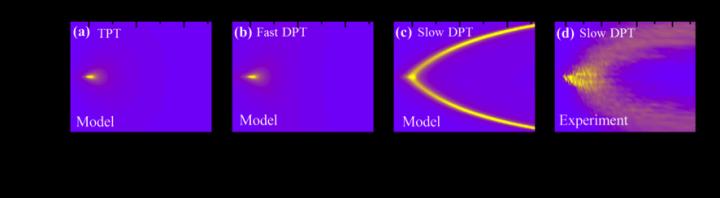
Surprisingly, the newly published work reported the most significant deviations to occur when the dynamics is slow. This is unexpected, because slow dynamics is generally understood to approach thermodynamic behavior, and most experimental studies of equilibrium properties are in fact slow dynamics studies, in which the external parameters are changed so slowly that the system can be presumed to be arbitrarily close to thermodynamic equilibrium conditions. However, the new work by Riego et al. shows that slow DPTs are very different from conventional TPTs, whereas fast DPTs exhibit the previously postulated full equivalency to TPTs.
In their now published work, the authors studied by means of experiments and computations the detailed behavior of a ferromagnetic system that mimics the kIM upon being subjected to a combination of an oscillatory magnetic field of amplitude H0 and period P, and a constant bias field Hb. When the field is swept fast, the magnetization M of the system cannot follow the field reversal and thus exhibits a nonzero cycle-averaged value Q= , which is the order parameter of the dynamic state. So far, Q(P,Hb ) diagrams of DPTs were assumed to be equivalent to M(T,H), diagrams for TPTs with T and H being the temperature and applied field, respectively. Concomitantly, the susceptibility diagrams were understood to be identical exhibiting a single sharp peak due to the susceptibility divergence at the critical point. However, the detailed study by the nanoGUNE researchers now shows that there are anomalous additional features occurring for DPTs in cases of slow dynamic phase transitions, which appear as susceptibility side-bands in the paramagnetic state, and for which no equivalency exists in TPTs. Only for fast DPTs, the equivalency to TPTs is preserved as can be seen in the figure.