Observing the quantum behavior of light is a big part of Alan Migdall’s research at the Joint Quantum Institute. Many of his experiments depend on observing light in the form of photons—the particle complement of light waves—and sometimes only one photon at a time, using “smart” detectors that can count the number of individual photons in a pulse. Furthermore, to observe quantum effects, it is normally necessary to use a beam of coherent light, light for which knowing the phase or intensity for one part of the beam allows you to know things about distant parts of the same beam.
In a new experiment, however, Migdall and his JQI colleagues perform an experiment using incoherent light, where the light is a jumble of waves. And they use what Migdall calls “stupid” detectors that, when counting the number of photons in a light pulse, can really only count up to zero, as anything more than zero befuddles these detectors and is considered as number that is known only to be more than zero.
Basically the surprising result is this: using incoherent light (with a wavelength of 800 nm) sent through a double-slit baffle, the JQI scientists obtain an interference pattern with fringes (the characteristic series of dark and light stripes denoting respectively destructive and constructive interference) as narrow as 30 nm.
This represents a new extreme in the degree to which sub-wavelength interference (to be defined below) has been pushed using thermal light and small-photon-number light detection. The physicists were surprised that they could so easily obtain such a sharp interference effect using standard light detectors. The importance of achieving sub-wavelength imaging is underscored by the awarding of the 2014 Nobel Prize for chemistry to scientists who had done just that.
The results of Migdall’s new work appear in the journal Applied Physics Letters (1). Achieving this kind of sharp interference pattern could be valuable for performing a variety of high-precision physics and astronomy measurements.
BEATING THE DIFFRACTION LIMIT
When they pass through a hole or past a material edge, light waves will diffract—that is, a portion of the light will fan out as if the edge were a source of waves itself. This diffraction will limit the sharpness of any imaging performed by the light. Indeed, this diffraction limitation is one of the traditional features of classical optical science dating back to the mid 19th century. What this principle says is that in using light with a certain wavelength (denoted by the Greek letter lambda) an object can in general be imaged with a spatial resolution roughly no finer than lambda. One can improve resolution somewhat by increasing lens diameters, but unless you can switch to light of shorter lambda, you are stuck with the imaging resolution you’ve got. And since all the range of available wavelengths for visible light covers only a range of about 2, gaining much resolution by switching wavelengths requires exotic sources and optics.
The advent of quantum optics and the use of “nonclassical light” dodged the diffraction limit. It did this, in certain special circumstances, by considering light as consisting of particles and using the correlations between those particles
The JQI experiment starts out with a laser beam, but it purposely degrades the coherence of the light by sending it through a moving disk of ground glass. Thereafter the light waves propagating toward the measuring apparatus downstream originate from a number of places across the profile of the rough disk and are no longer coordinated in space and time (in contrast to laser light). Experiments more than a decade ago, however, showed that “thermal” light (not unlike the light emitted haphazardly by an incandescent bulb) made this way, while incoherent over long times, is coherent for times shorter than some value easily controlled by the speed of the rotating ground glass disk.
Why should the JQI researchers use such thermal light if laser light is available? Because in many measurement environments (such as light coming from astronomical sources) coherent light is not available, and one would nevertheless like to make sharp imaging or interference patterns. And why use “stupid” detectors? Because they are cheaper to use.
THE EXPERIMENT
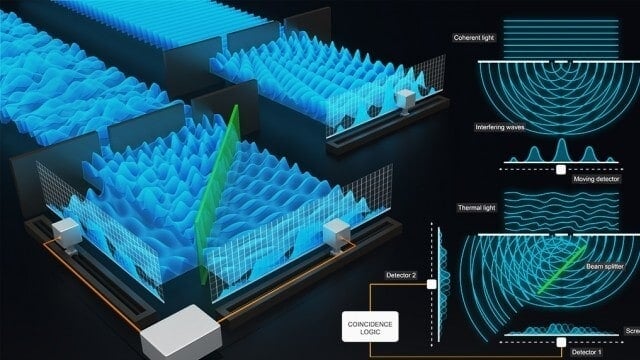
In the case of coherent light, a coordinated train of waves approach a baffle with two openings (figure, top). The light waves passing through will interfere, creating a characteristic pattern as recorded by a detector, which is moved back and forth to record the arrival of light at various points. The interference of coherent light yields a fixed pattern (right top in the figure). By contrast, incoherent light waves, when they pass through the slits will also interfere (lower left), but will not create a fixed pattern. Instead the pattern will change from moment to moment.
In the JQI experiment, the waves coming through the slits meets with a beam splitter, a thin layer of material that reflects roughly half the waves at an angle of 90 degrees and transmits the other half straight ahead. Each of these two portions of light will strike movable detectors which scan across sideways. If the detectors could record a whole pattern, they would show that the pattern changes from moment to moment. Adding up all these patterns washes out the result. That is, no fringes would appear.
Things are different if you record not just the instantaneous interference pattern but rather a correlation between the two movable detectors. Correlation, in this case, means answering this question: when detector 1 observes light at a coordinate x1 how often does detector 2 observe light at a coordinate x2?
Plotting such a set of correlations between the two detectors does result in an interference-like pattern, but it is important to remember that this is not a pattern of light and dark regions. Instead, it is a higher order effect that tells you the probability of finding light “here” given that you found it “over there.” Because scientists want to record those correlations over a range of separations between “here” and “over there” that includes separations that pass through zero, there is a problem. If the two locations are too close, the detectors would run into each other.
To avoid that a simple partially silvered mirror, commonly called a beam splitter, effectively makes two copies of the light field. That way the two detectors can simultaneously sample the light from virtual positions that can be as close as desired and even pass through each other.
And what about the use of stupid detectors, those for which each “click” denoting an arrival tells us only that more than zero photons have arrived? However, here the time structure of the incoming light pulse becomes important in clarifying the measurement. If we look at a short enough time, we can arrange that the probability of more than one photon is very low, so a click tells us that with good accuracy that indeed just one photon has arrived. But then if we design the light so that its limited coherence time is larger than the recovery time of our stupid detectors, it is possible for the detector to tell us that a specific number of photons were recorded, perhaps 3 or 10, not just the superfluous “more than zero” answer. “In this way, we get dumb detectors to act in a smart way,” says Migdall.
This improved counting the number of photons, or equivalently the intensity of the light at various places at the measuring screen, ensures that the set of correlations between the two detectors does result in an interference-like pattern in those correlations. Not only that, but the fringes of this correlation pattern—the distance between the successive peaks—can be as small as 30 nm.
So while seeing an interference pattern could not be accomplished with dumb detectors, it could be accomplished by engineering the properties of the light source to accommodate the lack of ability of the detectors and then accumulating a pattern of correlation between two detectors.
Considering that the incoming light has a wavelength of 800 nm, the pattern is sharper by a factor of 20 or more from what you would expect if the diffraction limitation were at work. The fact that the light used is thermal in nature, and not coherent, makes the achievement more striking.
This correlation method is not the same as imaging an object. But the ease and the degree to which the conventional diffraction resolution limit could be surmounted will certainly encourage a look for specific applications that might take advantage of that remarkable feature.