To investigate the influence of gravity on the propagation of light, researchers usually have to examine astronomical length scales and huge masses. However, physicists at Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) and Friedrich Schiller University Jena have shown that there is another way. In a recent issue of the journalNature Photonics they find the answers to astronomical questions in the laboratory, shifting the focus to a previously underappreciated material property – surface curvature.*
According to Einstein’s general theory of relativity, gravity can be described as the curvature of four-dimensional spacetime. In this curved space, celestial bodies and light move along geodesics, the shortest paths between two points, which often look anything but straight when viewed from the outside.
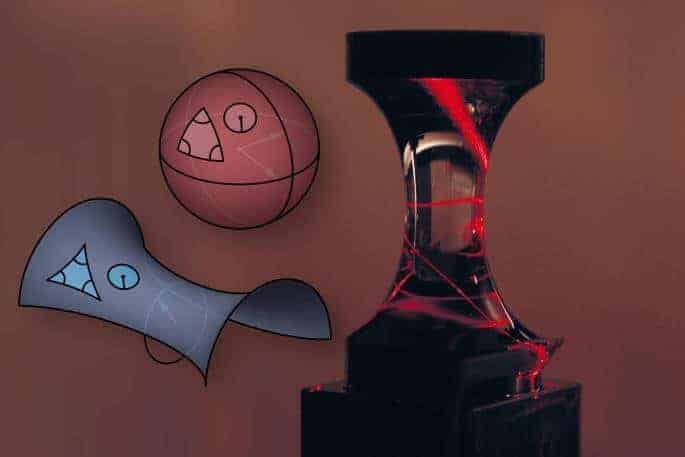
The team of researchers led by Prof. Dr. Ulf Peschel from Friedrich Schiller University Jena used a special trick to examine the propagation of light in such curved spaces in the laboratory. Instead of changing all four dimensions of spacetime, they reduced the problem to two dimensions and studied the propagation of light along curved surfaces. However, not all curved surfaces are the same. ‘For example, while you can easily unfold a cylinder or a cone into a flat sheet of paper, it is impossible to lay the surface of a sphere out flat on a table without tearing or at least distorting it,’ says Vincent Schultheiß, a doctoral candidate at FAU and lead author of the study. ‘A well known example of this is world maps that always show the surface in a distorted way. The curvature of the surface of a sphere is an intrinsic property that can’t be changed and has an effect on geometry and physics inside this two-dimensional surface.’
The researchers examined the effects of this intrinsic curvature of space on the propagation of light in their experiment. To do so they captured light in a small area close to the surface of a specially made object and forced it to follow the course of the surface. As the light propagated it behaved in the same way that it does when deflected by huge masses. By changing the curvature of the surface it is possible to control the propagation of light. Conversely, it is also possible to learn about the curvature of a surface itself by analysing the propagation of light. When transferred to astronomical observations, this means that light that reaches us from far away stars carries valuable information about the space that it has travelled through.
In their work the researchers studied intensity interferometry, pioneered by the English physicists Robert Hanbury Brown and Richard Twiss, which is used to determine the size of stars that are close to the sun. In this measurement technique, two telescopes are set up some distance apart and focused on the star that is to be examined. The fluctuations in light intensity measured by the two telescopes are then compared. Fluctuations in intensity are a result of the interference of light emitted separately from the surface of the star – visible as a pattern of light dots in the images produced – and allow conclusions to be drawn about the size of the object that is observed.
As paths of light in curved space tend to converge or diverge much more frequently than in flat space, the size of the dots changes depending on the curvature. The researchers were able to show that knowing the curvature is crucial for interpreting results and that experiments that use interferometry are suitable for measuring the general curvature of the universe more exactly.
Whether the results of their research will lead to a better understanding of the universe is still written in the stars. ‘The main goal of our research is to transfer findings based on the general theory of relativity to materials science by carefully modelling the surfaces of objects,’ Professor Peschel says. Although these two fields seem rather unrelated at first glance, there are some important connections. ‘From a manufacturing point of view, flat designs are often much easier to achieve. However, curved surfaces have a potential that has not yet been exploited and could be used to control light paths in optical systems, for example. Creating local variations in the surface curvature can often have the same effect as changing the volume material itself. This could allow the number of steps required and materials used when manufacturing integrated optical circuits or micro-optic components to be reduced.’