Key Points
- Scientists have developed a model nanomagnetic array to explore the physics of collective behaviour.
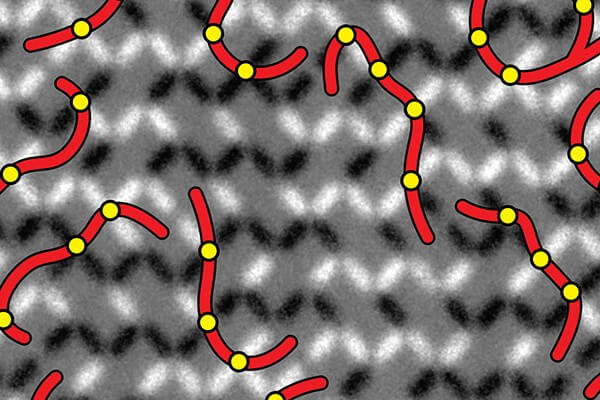
- The array is made up of strings of connected points of high energy among the lattice, which are limited to certain endpoints and connect to those endpoints in particular ways.
- This constraint on the strings’ behaviour is an example of what physicists call topological behaviour.
Scientists have designed and measured a model nanomagnetic array to explore the physics of collective behaviour.
This array consists of connected strings of high energy among the lattice, which can stretch and shrink, but also reconnect. These strings are limited to certain endpoints and must connect to those endpoints in particular ways. This constraint on the strings’ behaviour is an example of what physicists call topological behaviour. This work was done by a multi-institutional team and was published in a paper in Science.
“This system is an instance in which topologically driven features appear in a purely classical material system—that makes them easier to study and characterize,” said Yale applied physics professor Peter Schiffer, one of the authors of the work.
The team for this study included researchers from Los Alamos National Laboratory, Yale University, and the University of Minnesota. They developed a geometry called Santa Fe spin ice, inspired by the shapes in a brick floor in Santa Fe, New Mexico, and fabricated it first theoretically at Los Alamos, and then experimentally at Yale and the Advanced Light Source at Berkeley National Laboratory.
At high temperatures, the researchers observed the merging and reconnecting of strings, resulting in the system transitioning between topologically distinct configurations. But below a crossover temperature, the string motion was limited to simple changes in length and shape. Therefore, the work shows that there is a dynamical crossover: below a certain temperature those topologically non-trivial moves become suppressed, and only the topologically trivial (wiggling, extending, contracting) remain.
“This level of insight is unusual for any system, and it sets the stage for other topological studies in the future,” said Schiffer.