Forward
The following is a more developed version of the paper I posted on Science Blog about a year ago. I describe the motion of mass in time with a more visual example, and I give a more detailed alternative account of Young’s double-slit experiment. I’ve also added a section linking the hypothesis with the energy commonly attributed to gravitation.
Abstract
It is proposed that light is at absolute rest, its apparent motion being the reflection of the motion of mass in time. The hypothesis resolves the paradox of the apparent wave/particle duality of light, accounts for its speed being invariant and a limit, explains other peculiarities of its behavior, and identifies the source of gravitational energy.
Introduction
Light is currently regarded as in some ways wavelike, in some ways particle-like, invariant in speed, the limit of speed, and having various strange non-local effects. Einstein’s suggestion (1905) that light be accepted as both wavelike and particulate pending an intelligible resolution of the evidence has become an abiding commitment to paradox as quantum theory has expanded the range of the counter-intuitive to encompass much of theoretical physics. Nonetheless, the value of the fundamental scientific preference for simplicity of description, explanatory power, and logical coherence remains, in principle, as desirable as ever. However much science is now accommodated to the paradoxical features of light, a theory that would obviate a need for strange compromise is always to be preferred by scientific standards.
The idea that light might be at absolute rest seems no doubt a very odd and unlikely remedy at first impression, but I hope to justify it here by an appeal to the explanatory power by which it may be judged superior to the conventional view.
A Heuristic Graphic
A simple spacetime diagram (figure 1a) conforming to Special Relativity and the Lorentz transformations(1), and drawn according to the relativistic perspective of a single observer, provides a heuristic representation by which the present hypothesis might be most readily understood.
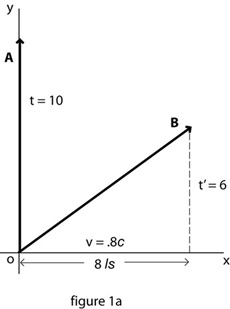
The x-axis represents space, while its perpendicular, the t-axis, represents time – both according to observer A, who is considered to be at rest and moving in time(2) along the t-axis. Vector B represents a body in motion relative to A.
A travels 10 sec (3) in time in the scope of the diagram while “at rest” in space. Body B, which as a matter of convenience is located initially at o, moves from the vicinity of A at a velocity, according to A, which takes it 8 ls in 10 sec. The final coordinates of B (8,6) can be derived from the Lorentz transformations, or geometrically by means of measuring the lengths in the diagram. By locating B at 6 seconds in time it is represented that the clock of B has moved 6 sec in the reference frame of A.
The spacetime interval given by s2 = t2 – x2 (with t proportional to c) is expressed here by
s2 = 102 – 82
s2 = 62
Thus s, the interval as it is generally called, is represented in the diagram as the proper time of body B.
A significant implication of the diagram is that there are actually two invariants involved in a relativistic relationship: the conventionally recognized interval, the proper time of B, and in addition, the identical spacetime intervals of the world-lines of A and B. The world line of an observer is not commonly recognized as being equivalent in length to the interval of the world-line of a body being observed; but in the relationship shown in figure 1a between an observer and a body in relative motion (where t2 = s2 + x2), the spacetime interval of the observer is necessarily equivalent to any world-line in relative motion, as the latter forms the hypotenuse of the Euclidean triangle described by the observer’s measure of another body’s distance traveled in space and the time elapsed on the moving body’s clock.
It is important to note that both the Lorentz Transformations and the equation for the invariant interval indicate a Euclidean relationship between space and time, and between bodies in relative motion. Although the relationship between clocks in relative motion given by t’ = (t2 –x2).5 is indeed parabolic, as is generally recognized, the fact that a hypotenuse relates to the sides of a Euclidean triangle by a parabolic function presupposes the right-angle. And as figure 1a shows, the temporal component of any body’s uniform motion in spacetime is at a right-angle to the observer’s space axis.
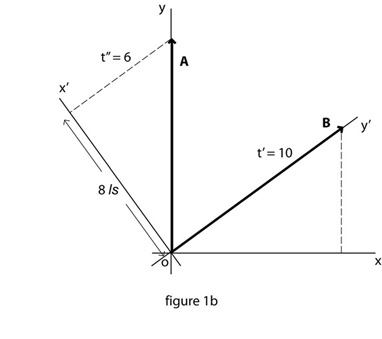
Figure 1b shows both reference frames at once, with A and B each moving in time, and perpendicular to space according to its own frame. The perpendicular relationship of a body’s motion in time to its own reference in space will be significant in later considerations.
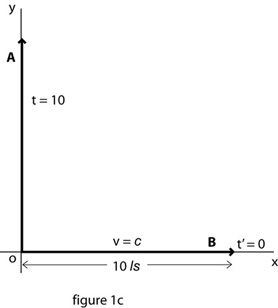
The relative motion of light as it would be represented in these terms is especially noteworthy. And it should be kept in mind that whereas the speed of light is commonly expressed as (approximately) 300,000 km per second, or 1 ls, to fully describe its observed motion relativistically is to report that it travels 1 ls in space relative to an observer’s spatial reference, and zero seconds in time relative to the observer’s temporal reference, as is given both by the Lorentz transformations and the equation for the spacetime interval. A world-line representing a ray of light in figure 1c, depicted below, therefore has a spacetime interval of 10 but a proper time of zero, and lies directly along the x-axis of observer A. (The interval in this case is s2 = 102 – 102.)
Two preliminary conclusions derived from these diagrams can be mentioned:
The speed of light as a limit: If the world-lines of bodies in relative motion are understood as having the same spacetime interval but with varying spatial and temporal components according to their relative spacetime trajectories, the limiting spatial velocity is the interval of a world-line along the space axis measured in terms of the same interval along the corresponding time axis. A vector drawn along the x-axis in figure 1c to represent a ray of light extends as far along the x-axis as time elapses for the observer in the duration of the diagram. There is no vector that can extend further in space than one that has a temporal component of zero.
The speed of light as invariant: Due to the invariance of the observer’s and observed spacetime intervals, each observer will measure light as traveling the same distance in space as time elapses in that observer’s reference frame, and though the measure of the spatial distance traveled by a beam of light between events will vary between reference frames, the rate will always be agreed upon. We can also infer from the observation of light as projected in figure 1c that distance in time is equivalent to distance in space – that one second in time is the same distance, but in a perpendicular direction, as 300,000 km in space.
The Hypothesis
The fact that the motion of material bodies is relative, and limited below c, while the motion of light is invariant, and the absolute limit c, suggests a fundamental distinction. If motion in time were to be regarded as a correlate of mass, if the clock of a material body is unable to stop entirely, and if in contrast light is massless, and its clock (if it could be said to have one) is invariably motionless, then light could be construed as actually, absolutely, not-moving in time. And if light doesn’t move in time, it seems meaningless to say that it moves at all.
The question is: If light is considered to be at absolute rest, if the apparent motion of light is actually the reflection of the motion of mass in time, however absurd the idea may seem at first, then what paradoxes could be resolved, what potential exists for a more comprehensive understanding of other issues and phenomena? What if material (massive) bodies exist in spacetime, but photons are embedded in space? What would be the implications if light is at absolute rest, and if the motion of mass in time – perpendicular to space and yet always in space – is the basis of all motion, real and apparent?
To represent light in these terms, figure 1d depicts a photon B as stationary, located in space, and according to A, 10 ls distant from the origin o. B is absorbed by A as the latter moves in time at the intersection of t = 10.
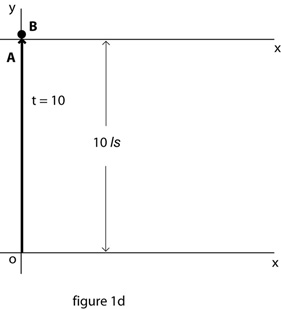
Note that A is always in space, hence the x-axis actually follows the motion of A in time and is depicted both at the origin and the end of the duration represented in the diagram.
A further deduction
If motion in time is regarded as perpendicular to the spatial dimensions, such motion would arguably have two aspects: To move perpendicular to the spatial (directly away from or toward any three-dimensional point) could be described as a concentric, wavelike motion relative to each point in space – because only a concentric radiation (away from) or concentration (toward), in the spatial aspect of a four-dimensional motion in spacetime could be considered perpendicular to a point in three dimensions at once. But since four-dimensional motion in the spacetime continuum would always remain in space as it moves across space, the motion would also involve a trajectory across definite spatial points. Therefore, a body moving in time could be described as continuously radiating from a series of points in space, and concentrating upon those it approaches.
If the photon is regarded as a spatial (a-temporal) object embedded in space, an observer who regards herself as at rest, and light as moving, while actually moving across space in time, will experience direct interactions with photons as impacts with moving particles, and will experience indirect interactions as the manifestations of waves. The apparent wave/particle duality of light would reflect the observations and interactions of bodies moving in spacetime with other bodies (photons) embedded in space.
We could therefore describe motion in time as a motion literally across space, a continuous radiation from one point in space and a concentration upon another. The apparent motion of light would in this hypothesis be the reflection of an observer’s motion in time and across space.
Let’s consider what else might be explained by this hypothesis that cannot be otherwise explained, or cannot be explained as well.
Implications
As already stated, the most significant implication of the present hypothesis is that the definition of light as being a-temporal and at absolute rest permits the resolution of the wave/particle paradox, a problem that has long eluded satisfactory explanation. If a body that exists in time is said to be moving perpendicular to space and yet to occupy a definite position in space at each moment, wave/particle duality can be attributed to our experience of the interaction between mass and light under different conditions – the wavelike radiation from, or relative to, one point, and the point-like intersection with another.
Given the hypothesis that mass, by moving in time, moves across space in a manner that places it always in space while also moving perpendicular to the spatial dimensions, in order to account for the variable wavelike behavior we observe with light it seems necessary to posit the four-dimensional motion of mass as a trajectory that fluctuates in a cyclic manner along the surface of its radiation. (For the sake of simplicity, the motion of mass relative to space will be treated in what follows as just a correlative radiating and revolving trajectory, without further specification. The precise characteristics of such motion is a question for experimentation and mathematical treatment.)
As Special Relativity suggests, and as the foregoing diagrams express, space and time are evidently co-metric. A body in relative motion moves relatively less in time the more it moves in space. Therefore, if light is three-dimensional, and embedded within a four-dimensional continuum, its spatial orientation within spacetime may vary according to the circumstances of its emission. Depending on a photon’s spatial orientation relative to a massive body, the latter may approach the former in a relatively more-or-less spatial, more-or-less temporal orientation, resulting in a more-or-less contracted spatial separation, and therefore, a greater or lesser wavelength and frequency. The wavelength and frequency we associate with light might thus be attributed to the relative interval between cycles of the radial trajectory of mass. We might envision a four-dimensional radial motion as a spiraling in which each “wavelength” represents a cyclic return to a particular three-dimensional trajectory, and we might attribute the apparent polarity of light to a reflection of the spiraling of mass across space along two dimensions of its wave-front.
An obvious question raised by the hypothesis is how to characterize the relationships among material bodies as they move in time and across space. It seems most plausible and consistent with our experience that material bodies, if at rest relative to each other, would move in a more or less synchronous radiation along parallel trajectories, so that the spatial aspect of their motion in time would be imperceptible, and relative locations of mass in space would remain constant. It may be significant that small variations in phase would be expected to produce wavelike phenomena like those originally predicted for material bodies by de Broglie (1924).
Perhaps the most vexing difficulty in comprehending the present hypothesis is imagining the relationship between various masses, and light, when the light-source is envisioned in their midst. Consider a room with a light-source in the center and a number of observers arranged against the four walls. In this situation we would describe the light-source as depositing a series of photons in space while the source, the observers, and every mass in the room is radiating across space, all in parallel with each other, because each is at a relative state of “rest.” For each photon deposited, there will eventually be an intersection with a mass (an atom) according to which of the spatial trajectories of the masses in the room is oriented toward the photon as its temporal wavefront crosses the photon’s location.
The strangeness of the relationship between light and mass can be illustrated by means of Young’s classic experiment with light (1803), which uses slits or pinholes in screens to produce seemingly inexplicable manifestations of simultaneity, non-locality, and interference. As is well-known, photons have been found to behave differently when passing through a slit in a screen depending on whether there is another slit some distance away.
Young’s experiment is depicted in the conventional manner in figure 2, treating light as moving and mass at rest:
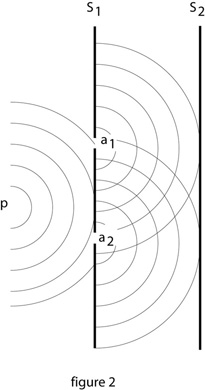
Point p represents a light-source, a1 and a2 are slits in screen s1, and s2 is a second screen where the light from p that “passes through” the slits is absorbed.
In terms of the present hypothesis, a screen can be regarded as a plane of material bodies (atoms), each of which might intersect, or not, with a photon depending on the distances of each material body from the light source as the photon is deposited, the spatial orientation of the photon (determining the relative wavelength of the masses), and the spatial trajectory of each mass at the moment its wave-front crosses the location of the photon. The light that “passes through” a slit in a screen will be specifically out of phase with all the trajectories of the masses of the screen, as the latter radiate across the space between the screen and light source.
The relationship just described between a photon and the first screen is represented in figure 3:
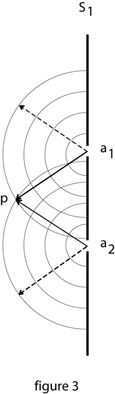
The semicircles represent spacetime wavelengths, along which spatial trajectories transmit, presumably returning to the same trajectory once per each wavelength. The solid vectors emanating from the slits a1 and a2 represent the trajectories of masses at the slits if they are closed, or the missing trajectories that would allow the photon to “pass” the screen if the slits are open. The dashed vectors represent the trajectories of the relative position of each slit when the wavefront of the other intersects with p. Whether a photon “passes” a slit in the screen or is absorbed by the screen is determined by the moment of emission, the distance between the source and an atom in the screen, and the wavelength of the screen relative to the spatial orientation of the photon.
Figure 4 represents the relationship between photons from the source that have intersected with one or the other slit at s1 to impinge on s2. The waves emanating from s2 represent the motion of atoms b1 and b2. Screen s1 is depicted with dashed lines to emphasize that it is radiating in parallel with s2, not being (as it might appear) intersected by the masses of s2.
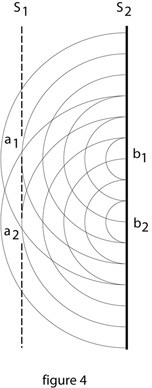
If only one slit is open, a series of photons will impinge on s2 in an intelligible manner, tending to group in a region of s2 closest to the slit, determined as in the non-intersection of photons with s1, by factors of time, distance, and wavelength. When a second slit is opened, the curious phenomenon first noticed by Young is the appearance of an interference pattern on s2, suggesting that the particles of light are suddenly behaving like waves. But in terms of the present hypothesis, with atoms in the screen conceived as radiating toward the photons, the phenomenon can be explained by an exclusionary principle that would limit absorption by atoms of photons to, perhaps, once per cycle, and the consequent preemption of absorption by atoms at one location by atoms at another: If for example with the opening of slit a2, atom b2, being closer to a2 than a1, tends to absorb photons from a2, sometimes instead of photons from a1. And having absorbed a photon from a2, if the photon it would otherwise have absorbed from a1 is preempted by some other atom (not b1), b2 is available to preempt the absorption of a photon from a1 that would otherwise be absorbed by b1. The particularities of photons that have avoided absorption in s1 – their orientations in spacetime, the coincidence of the moment of their emission with the trajectories of the masses in the screens, will determine a pattern of preemption in their absorption at s2. Thus, the dark regions appearing on s2 with the opening of slit a2, as if due to interference, can be interpreted as locations where intersections with photons are preempted by other masses due to harmonics of time, distance, and wavelength.
There is no basis in the present hypothesis for actual interference between or among photons and material bodies. If photons don’t actually move, and if material bodies radiate approximately in-phase, with only minor variations at the subatomic level, their apparent interference can be no more than a pattern, as on a screen, that we identify by analogy with interference found in material media. What is commonly called electromagnetic interference would be described instead as the manifestation of regularities in photon emission that makes intersection with masses at consistent distances moving along particular trajectories more or less likely. Similarly, light can be considered coherent when photon emission is precisely sequenced and oriented in space to be intercepted by masses along specific trajectories at regular wavelengths.
Another important aspect of light that has defied explanation is its peculiar non-local behavior, often described as quantum entanglement. It has been confirmed, in terms of the conventional concept of light, that a photon propagates in an expanding wave of probability that might be intercepted at any point on its wave-front, even if the wave-front is light-years in diameter. Bell (1964) has demonstrated that a correlation between a pair of photons can be instantaneous and indifferent to distance. We could account for such non-local phenomena in terms of the hypothesis by recognizing the motion of our analyzers and detectors as moving across space relative to the photons, and we could define locality at any moment in terms of the parallel trajectories of the components of the apparatus along their expanding wave-fronts. The otherwise incomprehensible simultaneities associated with light could thus be attributed to manifestations of motion in time perpendicular to space, whereby a point in space becomes an expanding sphere, and a contracting sphere becomes a point.
Other phenomenal aspects of light, such as reflection, diffraction, and its apparent retardation in various media can be explained, if the hypothesis is confirmed, in terms of the physics of absorption and re-emission at the atomic level, and needn’t detain us here.
Gravitational Energy
The hypothesis that mass, by moving in time, is in absolute motion across space, bears directly on the definition of gravitational energy.
With Einstein’s publication of General Relativity, gravitation was associated with the geometric distortion, “the curvature”, of spacetime in the presence of mass. This concept provided a most accurate description of orbital phenomena, and cosmological relationships in general. But the energy expressed when bodies directly interact due to the influence of gravitation – most commonly with the manifestation of weight pressing against a surface – does not immediately follow from the idea of spacetime geometry. Gravitation theory has accommodated the energy involved in gravitational phenomena by recourse to the pre-relativistic notion of a “force of gravity”, and by the development of mathematical analogies with electromagnetism. Various problems with the theoretical combination of geometry and force remain dubious, if not unresolved, as when a test particle in a box orbiting (accelerating around) the earth gives no indication of being acted upon by a force.
The problem may be best clarified by means of a thought-experiment:
Imagine two test bodies gravitating toward the earth from some considerable distance. For the sake of simplicity, consider the earth to be at rest and the test bodies to be gravitating directly toward its center of mass. (They appear to be simply “falling” from a perspective on the earth’s surface.) One body is an immense hollow sphere of negligible mass, the other is relatively small in size — an extra-vehicular scientist, let’s say — and also of negligible mass. Notice that while the test bodies are falling toward the earth (or more accurately, while the three bodies are converging) there is among them a purely relative transformation of potential energy to kinetic energy as each moves uniformly in its own frame of reference — there is, at least as yet, no occasion for an exchange of mass-energy in the form of the putative gravitational energy. Let the sphere and the scientist be placed initially close together so that as they approach the earth their geodesics (uniform motion in spacetime) converge enough to bring their surfaces in contact some time before the larger impact. (It is the fantastic size of the hollow sphere that allows the surfaces of the two bodies to meet somewhere above the earth’s surface). From the moment the sphere and the scientist come in contact until they reach the surface of the earth an inertial acceleration between them will intensify as each tries to conform to its own geodesic at an ever greater angle to the other. The situation will, if viewed in isolation, come to resemble the gravitation of a small body pressed against a planetary surface (although the gravitation between them is actually insignificant due to their negligible masses) and the scientist will even be able to stand upon the sphere. This development of an increasing inertial acceleration between the test bodies is the only aspect of the situation that changes from the moment they meet; the earthward component of their motion continues as before, a relative gravitation. Force has developed in the resistance to what is in this case a convergent gravitation of two bodies toward a third. And once the two reach the earth the situation remains essentially the same: Each one, now in conjunction with the entire conglomerate of the earth, presses toward the center of mass with the same sort of conflict of geodesics as was observed between them when they were gravitating from a distance. Along with the other components of the earth at and below the surface, they are resisted, and thereby accelerated, by those further below, due to the coincidence of the common inclination toward the center of mass and the subordinate obstructions.
The thought experiment illustrates that there is no evidence of energy in gravitation until geodesics come in conflict. The energy we associate with weight is not itself gravitational, it is an expression of the resistance to gravitation. Unlike when two relatively small free-moving bodies collide and diverge along new geodesics, when a body’s geodesic intersects with a sufficiently massive body, “gravitational energy”, as expressed in the conflict of gravitation and the resistance to gravitation, is relentless. How then does a geometric distortion produce a relentless dynamic?
In terms of the hypothesis that mass moves across space as it moves it time, the kinetic energy associated with that motion becomes conspicuous as the source both of the energy disclosed in the conflict of geodesics, and of the persistence of the energy expressed when a massive surface is encountered. The present hypothesis suggests that there is no need for a theoretical amalgamation of geometry and force to account for gravitational phenomena, and no need to invoke a “gravitational energy.” Whether free-moving or weighing against a massive body, the energy associated with gravitation is the kinetic energy, or if resisted, the impulsion, of mass moving in time. Gravitation as a geometric distortion of spacetime in the presence of mass brings the relentless motion of masses in-time and across-space into conflict. Gravitation in this view is entirely, and simply, geometry.
Conclusion
A relativistic spacetime diagram demonstrates that a two-dimensional projection of the four-dimensional continuum can illustrate the peculiar characteristics of light as the ultimate and invariant speed, and suggests that it is not meaningful to regard light as moving in either space or time. The hypothesis that light is at absolute rest, and that the apparent motion of light is the reflection of an observer’s own motion in time, has been shown to resolve the wave/particle paradox and to make intelligible the apparent non-local behavior of light. It also accounts for “gravitational energy” and reduces the description of gravitation to a geometrical effect. Although experimentation and mathematical formalization are needed to confirm and better define what has been described as the radial trajectory of mass in time across space, the necessarily dual and exotic nature of four-dimensional motion has been shown to make apparent characteristics of light such as wavelength, coherence, polarity, interference, and simultaneity more comprehensible as manifestations of the relative motion of mass, rather than light.
End notes
1. The Lorentz Transformations are t’ = (t-v)/(1-v2) .5 and x’ = (x-vt)/(1-v2).5, with t as time, x as distance, and v as velocity proportional to c.
2. It is permissible to say a body “moves” in time because spacetime has been recognized (by Minkowski, in the first place) as a continuum, as a corollary of Special Relativity. Duration in one coordinate system is a composite of motion in space and time according to another.
3. As a matter of convenience t is generally multiplied by c so that space and time can be expressed in distances of the same scale. I prefer instead to calibrate them by giving time in seconds (sec) and space in light-seconds (ls).
References
Bell J. (1964), “On the Einstein Podolsky Rosen paradox”, Physics 1 195-200.
de Broglie L. (1924), “Recherches sur la théorie des quanta,” Annales de Physique 3, 22-128, 1925, translated in Gunther L., Wave Mechanics, Pergamon, 1968.
Einstein A. (1905), In “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” (“On a Heuristic Viewpoint Concerning the Production and Transformation of Light”), Annalen der Physik 17:132-148.
Einstein A., Podolsky B., Rosen N. (1935), “Can quantum-mechanical description of physical reality be considered complete?” Phys.Rev. 47:777-80.
If our reporting has informed or inspired you, please consider making a donation. Every contribution, no matter the size, empowers us to continue delivering accurate, engaging, and trustworthy science and medical news. Independent journalism requires time, effort, and resources—your support ensures we can keep uncovering the stories that matter most to you.
Join us in making knowledge accessible and impactful. Thank you for standing with us!
